확률(probability)과 가능도(likelihood)
<핸즈온 머신러닝>(2편)을 읽다가 확률과 가능도에 대한 좋은 설명을 찾았다. 그동안 ‘최대 가능도 모델(또는 최대 우도 모델)’과 같은 용어를 접하면서도 이해가 쉽지 않았는데, 이 책에 간단하면서도 이해하기 쉬운 설명이 제시되어 있었다. 아래는 책 pp.337-339 까지의 내용이다.
확률(probability)과 가능도(likelihood)는 종종 구별 없이 사용됩니다. 하지만 통계학에서 이 둘은 다른 의미를 가집니다. 파라미터 $\theta$인 확률 모델이 주어지면 ‘확률’은 미래 출력 $\mathbf{x}$가 얼마나 그럴듯한지 설명합니다(파라미터값 $\theta$를 알고 있다면). 반면 ‘가능도’는 출력 $\mathbf{x}$를 알고 있을 때 특정 파라미터 값 $\theta$가 얼마나 그럴듯한지 설명합니다.
-4와 +1이 중심인 두 개의 가우시안 분포를 가진 1D 혼합 모델을 생각해보죠. 간단하게 나타내기 위해 이 모델은 두 분포의 표준편차를 제어하기 위한 파라미터 $\theta$ 하나를 가집니다. [그림]에서 왼쪽 위 그래프는 $x$와 $\theta$의 함수로 전체 모델 $f(x;\theta)$을 보여줍니다. 미래 출력 $x$의 확률 분포를 예측하려면 모델 파라미터 $\theta$를 지정해야 합니다. 예를 들어 $\theta$를 1.3(수평선)으로 설정했다면 왼쪽 아래 그래프와 같은 확률 밀도 함수 $f(x;\theta=1.3)$를 얻습니다. $x$가 -2와 +2 사이에 들어갈 확률을 예측하려면 이 범위에서 PDF의 적분을 계산해야 합니다(즉 그림자 부분의 면적). 하지만 $\theta$를 모른 채 대신 샘플 $x=2.5$(왼쪽 위 그래프에 있는 수직선) 하나를 관측했다면 어떻게 할 수 있을까요? 이 경우 오른쪽 위 그래프에 나타난 가능도 함수 $\mathcal{L}(\theta \vert x=2.5)=f(x=2.5;\theta)$를 얻습니다.
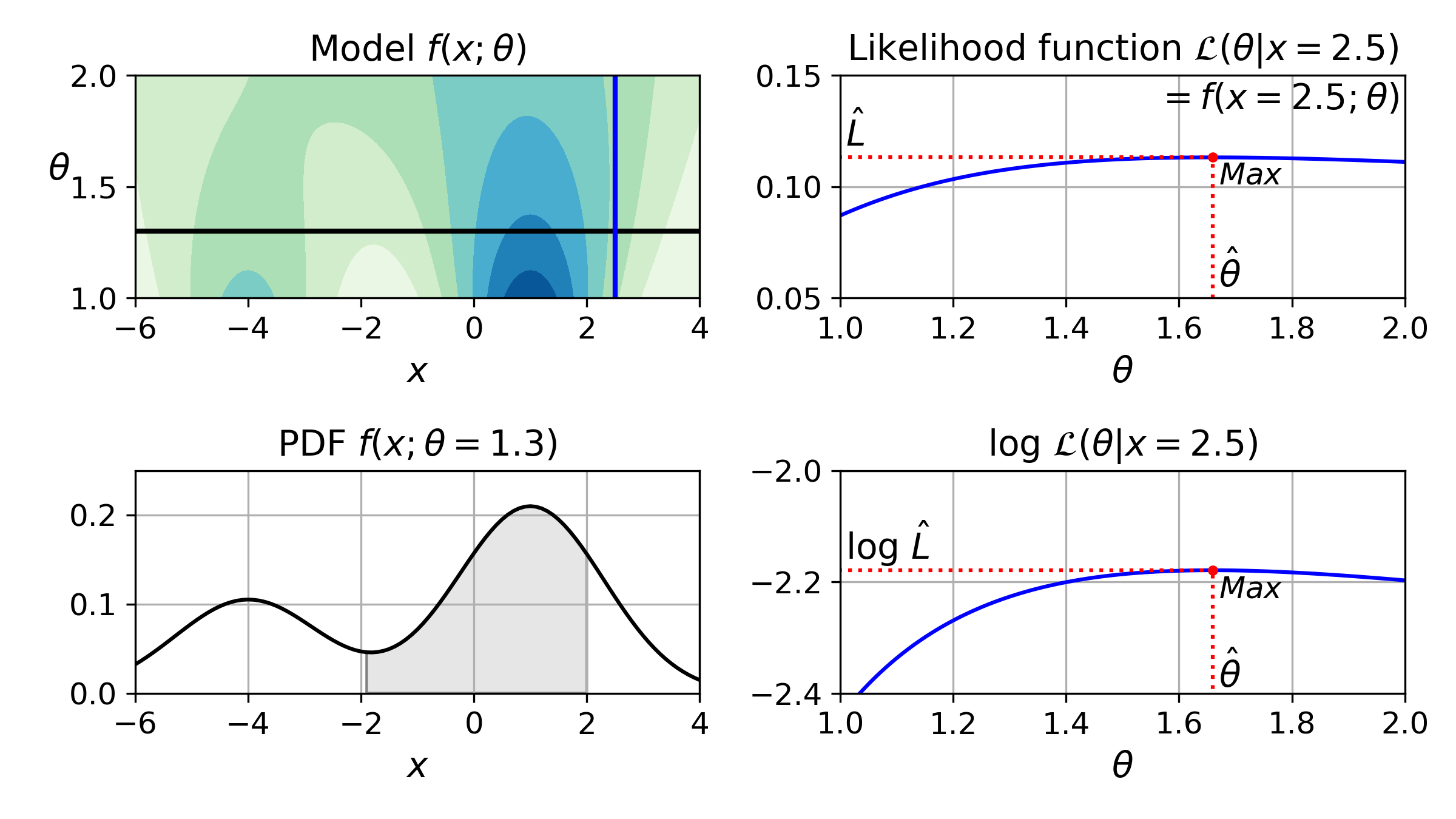
간단히 말해 PDF는 $x$의 함수입니다($\theta$ 고정). 반면 가능도 함수는 $\theta$의 함수입니다($x$ 고정). 가능도 함수가 확률 분포가 아니라는 것을 이해하는 것이 중요합니다. 가능한 모든 $x$에 대해서 확률 분포를 적분하면 항상 1이 됩니다. 하지만 가능한 모든 $\theta$에 대해서 가능도 함수를 적분하면 어떤 양수값도 될 수 있습니다.
데이터셋 $X$가 주어졌을 때 일반적으로 모델 파라미터에 대해 가장 그럴듯한 값을 예측합니다. 이를 위해 $X$에 대한 가능도 함수를 최대화하는 값을 찾아야 합니다. 이 예에서 샘플 $x=2.5$ 하나를 관측했다면 $\theta$의 최대 가능도 추정(maximum likelihood estimate)은 $\hat{\theta}=1.65^{[1]}$ 입니다. $\theta$에 대한 사전 확률 분포 $g$ 가 존재한다면 $\mathcal{L}(\theta \vert x)$를 최대화하는 것보다 $\mathcal{L}(\theta \vert x)g(\theta)$를 최대화하는 것이 가능합니다. 이를 최대 사후 확률(maximum a-posteriori; MAP)이라고 합니다. MAP가 파라미터 값을 제약하므로 이를 MLE의 규제 버전으로 생각할 수 있습니다.
가능도 함수를 최대화하는 것은 이 함수의 로그를 최대화하는 것과 동일합니다([그림] 오른쪽 아래 그래프). 로그 함수는 항상 증가하는 함수이기 때문에 $\theta$가 로그 가능도를 최대화하면 이는 가능도도 최대화합니다. 일반적으로 로그 가능도를 최대화하는 것이 더 쉽습니다. 예를 들어 여러 개의 독립적인 샘플 $x^{(1)}$에서 $x^{(m)}$을 관측했다면 개별 가능도 함수의 곱을 최대화하는 $\theta$를 찾아야 합니다. 하지만 로그 가능도 함수의 (곱이 아니라) 합을 최대화하는 것이 동일하면서도 훨씬 쉽습니다. 로그의 곱셈을 덧셈으로 바꿀 수 있는 성질 덕분입니다. 즉, $log(ab)=log(a)+log(b)$.
가능도 함수를 최대화하는 $\theta$값 $\hat{\theta}$을 추정하고 나면 AIC와 BIC를 계산하기 위해 필요한 값인 $\hat{L}=\mathcal{L}(\hat{\theta}, X)$를 계산할 준비가 됩니다. 이를 모델이 데이터에 얼마나 잘 맞는지 측정하는 값으로 생각할 수 있습니다.
[1] 책에서는 본문의 값과 그림 모두 1.5로 되어 있으나, 샘플 코드를 돌린 결과는 1.65 정도로 표시되어 그에 맞게 수정함.
결국에는 데이터를 확률 분포 모형에 fitting 한다는 얘기다. 즉 현실 세계를 관찰한 결과인 데이터는 손에 가지고 있지만, 그것이 어떤 원리(?)로부터 나왔는지는 알지 못하는 상황에 직면한 것과 같다. 이 상황에서, 기존에 축적된 지식으로부터 원리와 유사하다고 생각되는 모형을 선택한다. 이 모형은 파라미터값이 정해지지 않은(그래서 a나 b 등과 같은 알수 없는 값으로 표현된) 상태이다. 데이터를 바탕으로 해서 그 파라미터값을 찾아야만이 모형을 데이터에 맞춰 완성할 수 있고, 해당 데이터가 생성된 원리를 유추하는 모형을 손에 넣을 수 있다. 그렇게 모형을 데이터에 맞추는(fitting 하는) 방법 중 하나가 최대 가능도 추정(MLE)이라고 할 수 있다.